A Probabilistic Worldview via Applied Mathematics

Summary

Since the emergence of Newtonian mechanics as a classical natural philosophy, mechanics has become the paradigm for a scientific understanding of the objective world, with calculus as its language and forces as the "exogenous" cause of changing position by motion. The temporal continuum in term of the mathematical notion of real numbers plays a vital role here. Nevertheless, the definition of randomness in such a context has always been confusing. The emergence of probability theory less than 100 years old and its applications are now posing challenges for the discussion of the relationship between mathematics and physical reality, reviving some of the major questions in the philosophy of science from ancient Greece through the Renaissance. For example: Where does "truth" come from? What is randomness? How can we understand the phenomenon of life and the world through applied mathematics? Can we predict the future based on the past?

At the Berggruen Seminar, Qian Hong, Olga Jung Wan Endowed Professor of Applied Mathematics from University of Washington, Seattle, discussed these questions in his talk titled “A Probabilistic World View via Applied Mathematics”. Qian also shared with the audience his scientific understanding and philosophical views about probability and the pursuit of knowledge. Professor Qian obtained his B.A. in Astrophysics from Peking University and his Ph.D. in Biochemistry from Washington University in St. Louis. His main research areas include mathematical representations and modeling of biological systems, with a particular focus on using probability theory and statistical physics.

Professor Bai Shunong of the School of Life Sciences of Peking University, a Berggruen 2020-2021 fellow, was the moderator of the Seminar. Professor Bai has a particular interest in the living system and randomness in its evolution, and has published detailed research on this topic in the "Baihua" column. The research and scientific popularization efforts of both Bai and Qian are trying to challenge people's common understanding of "certainty", and they are also giving evidence and interpretation from a disciplinary perspective (biochemistry and biology).

The world from the perspective of mechanics

At the very beginning of his lecture, Professor Qian gave an example to illustrate that the prediction of the occurrence of an event in the future was way more complicated than we may believe.

Let's look at these numbers: “1, 1, 2, 3, 5, 8, 13…” What's the next number? We may determine a law that any number is the sum of its two preceding ones. In this way, the number following 13 should be 21. However, this figure might, alternatively, be the operation result of the polynomial formula shown in the figure below. This example demonstrates that our simple experience-based summary of the observed phenomena may be one-sided.

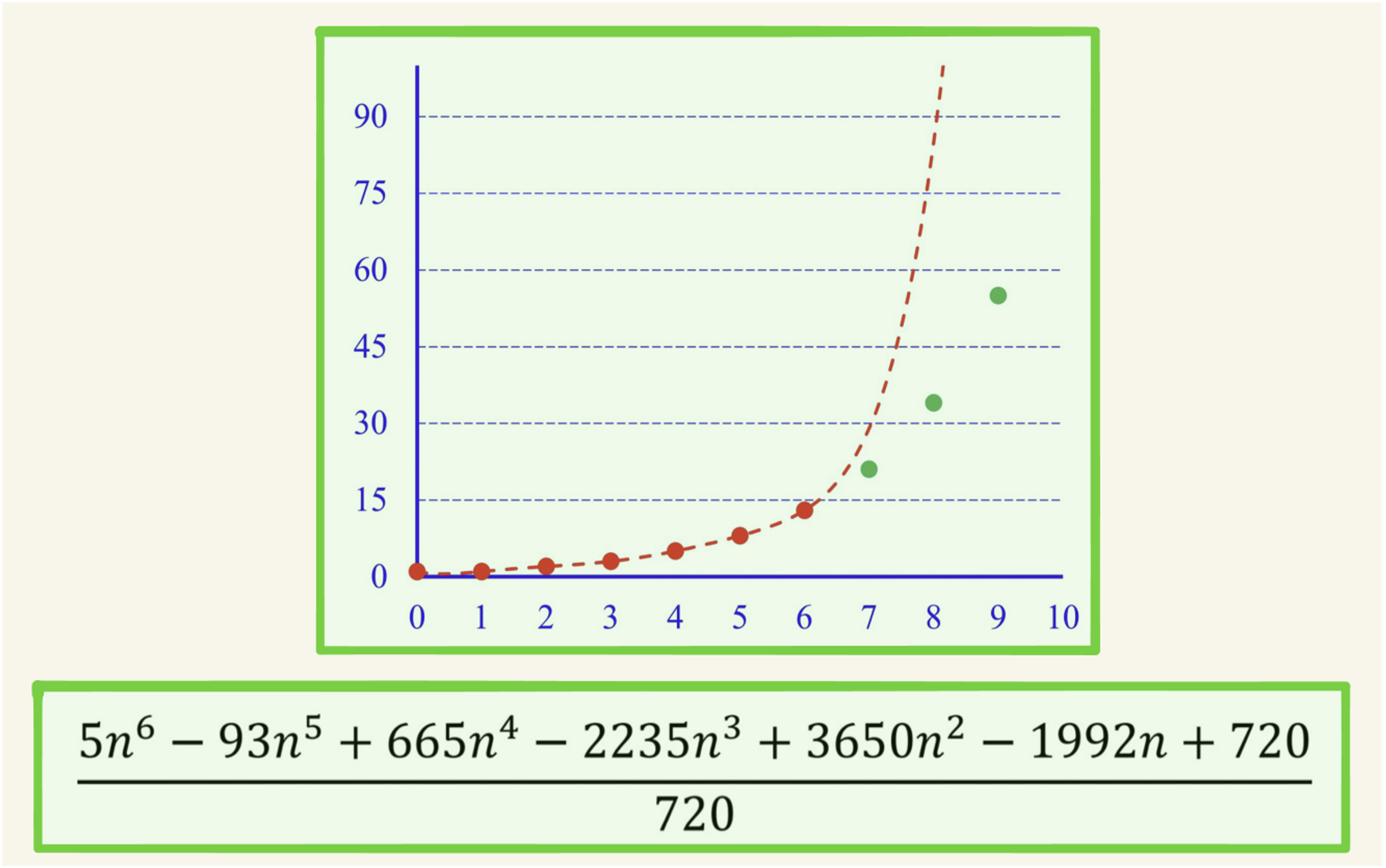
Professor Qian held that since Newton’s times, mechanics, the most fundamental scientific mechanism for our daily-life phenomena, has helped us understand the world. Similarly, mathematics’ notion of continuous time is an element in event prediction, as shown in the above example. Through the theory of mechanics, we are able to express the most important indicators used to measure all things in the world — energy — using calculus. This way, the infinitely complicated problems came down to one scalar function, and this function is enough to generate an infinitely complex world. The more energy you have, the longer you "live". There is a profound connection between energy and temporal continuity.

This way of understanding the world is closely related to Hilbert’s sixth problem among the twenty-three problems in mathematics published by mathematician David Hilbert in 1900.This question proposes mathematical treatment of the axioms of physics: The investigations on the foundations of geometry suggest the problem: To treat in the same manner, by means of axioms, those physical sciences in which already today mathematics plays an important part; in the first rank are the theory of probabilities and mechanics.

Professor Qian also pointed out, by quoting Roger Penrose, that when using mathematics, one had to do first was to discover how to disentangle the true from the suppositional in mathematics.This realization that the key to the understanding of Nature lay within an unassailable mathematics was perhaps the first major breakthrough in science.However, there is still a long way to go from the "truth" in mathematics to beyond the closed-loop operation that is based on hypothesis.

The concept of the probability wave was introduced as part of the quantum mechanics that emerged at the beginning of the 20thcentury and provided more paths for interpretation in the realm of mechanics. At the beginning of the 21st century, some scholars have come up again new hypothesis: Probability theory and entropic force might be the foundation of Newton’s law and gravity, but what is probability after all? What judgment and certainty do we have about probability?

Dispute between the frequentist school and the Bayesian school

In statistics, there are two dominating ideas for the interpretations of probability: Some argue that probability is the property (frequentist school) of a system (a body) itself; others argue that probability is a quantitative understanding of the world (Bayesian school).

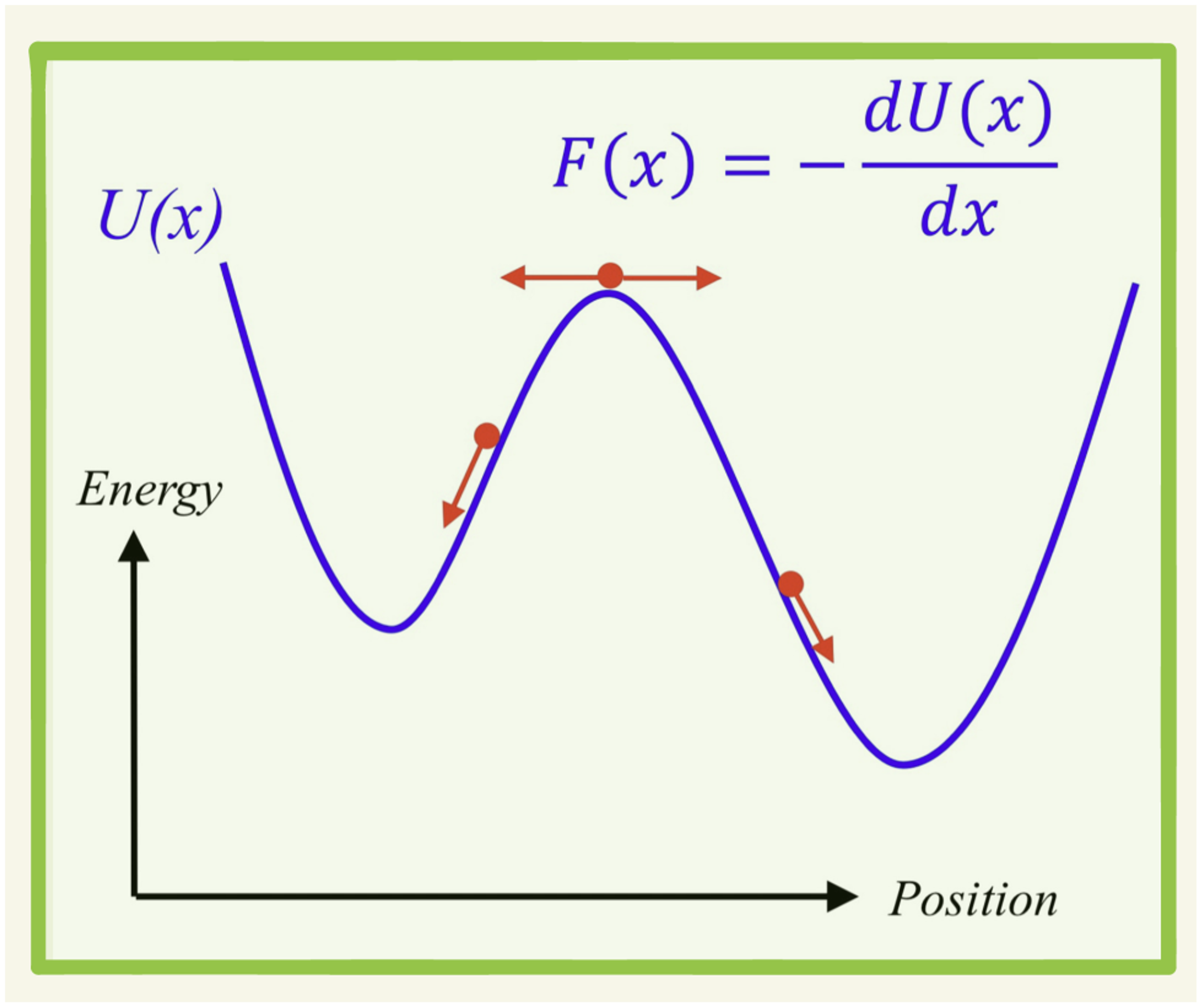
Within the framework of Newtonian mechanics, the randomness represented by probability has another name called "chaos". As shown in the figure below, the way a black spot changes and iterates in a complex system is "chaotic" to different extents. In a simpler system, the spot just changes its location. In a slightly more complicated closed system, what starts as a spot may turn into thin threads and end up covering the entire square without changing its total area. In a more "chaotic" circumstance, a spot may expand and then contracts, eventually covers everywhere in the square.

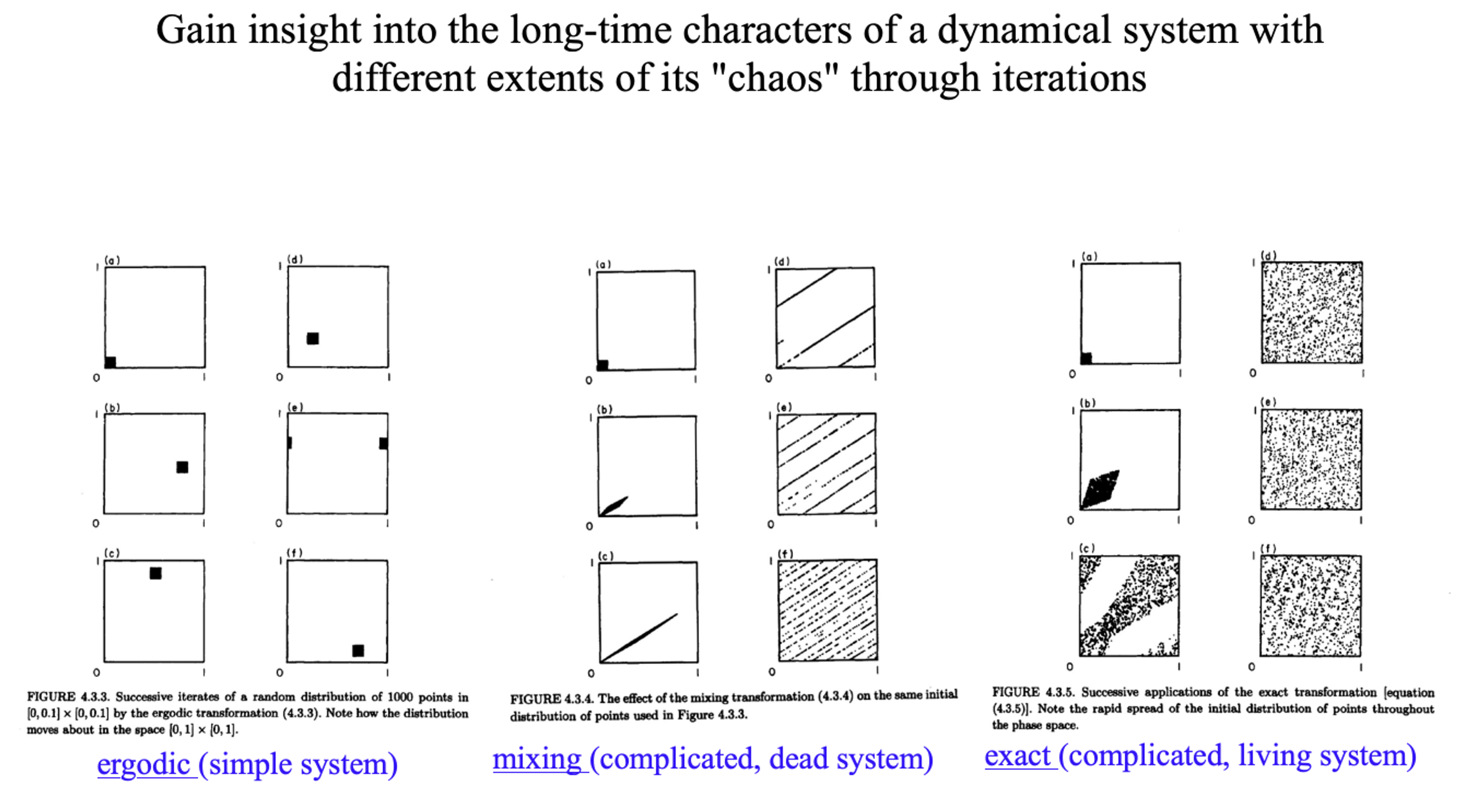
Mathematicians nowadays can characterize these different degrees of chaos in a more systematic way. For example, Andrey Kolmogorov put forward an axiomatic probability theory in 1934. Kolmogorov argued that to predict the probability of a future event, the first thing we need is a set of elementary events. This set includes all possible circumstances.

A question to be asked here is how we can deduce all possible circumstances. However, in the system of Newtonian mechanics, we know how atoms move forever ever after, as long as we know its current locations and velocities. In a similar way, mathematicians have also proved that when it comes to real numbers, there are only rational numbers and irrational numbers, and there cannot be any other numbers on the real number axis. To put it another way, if you believe in Newtonian mechanics and judgment of these mathematicians, we can indeed include all future events in one set.

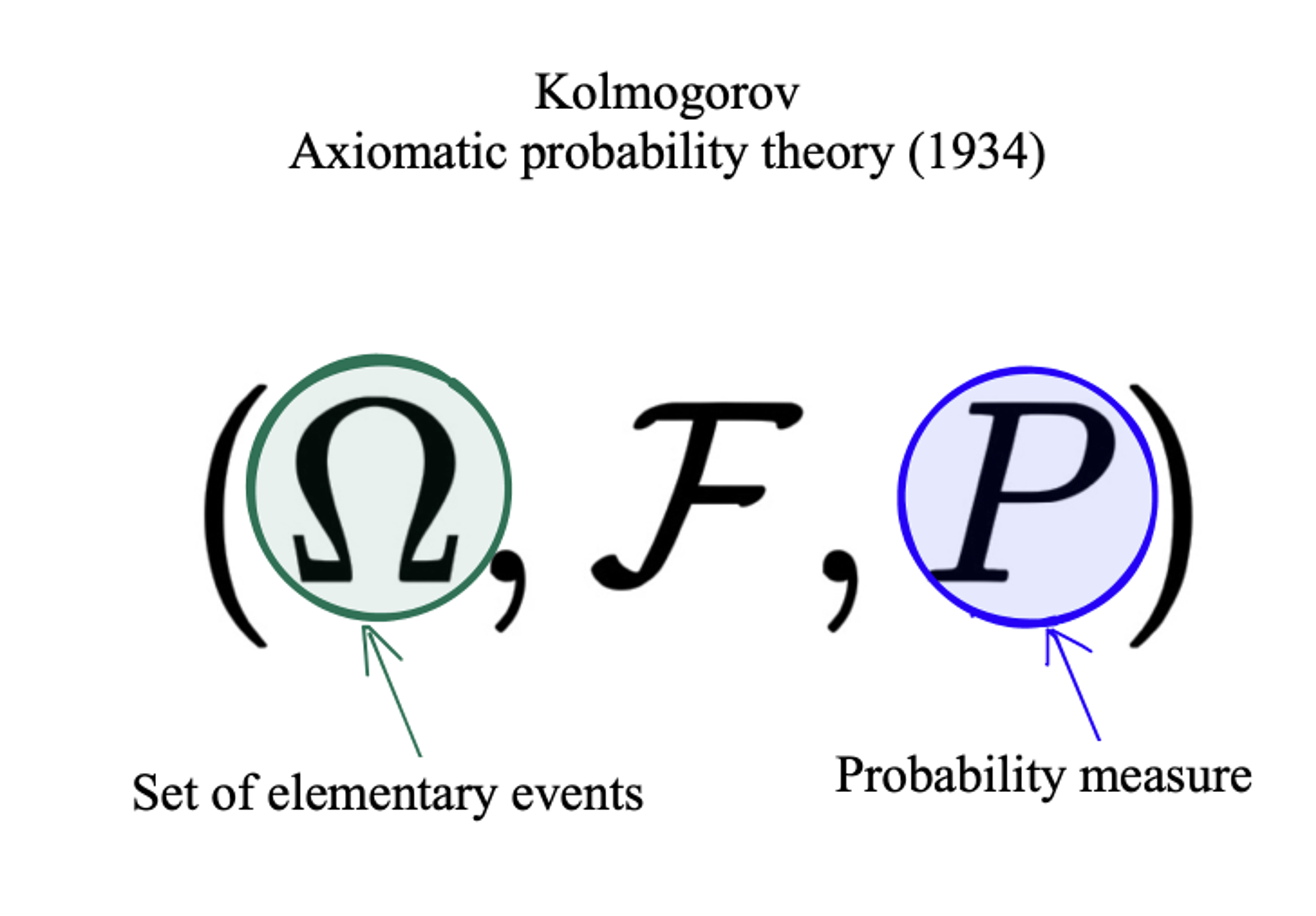
The set alone is not enough to predict the future. We need a probability measure as well. Colloquially, we may regard the probability measure as the weight of events in the set. Each elementary event has its weight, great or small, which represents the chance for its occurrence. This way, we may determine the probability of complicated event occurrence based on the elementary event and its probability measure, which ranges from 0 to 1, respectively, indicating never going to happen and definitely happening. Then a future prediction model is built.

Following an introduction to the axiomatic probability theory, Professor Qian used e the following example to illustrate different schools’ understanding of "probability":

• Zhang tossed a coin 10 times. The emblem showed up 9 times and the peony showed up 1 time. The conclusion is that ...

• Wang tossed 10 coins of the same production batch and got 9 emblems and 1 peony at the 5th coin. The 10 coins were all on the table. There is no probability anymore!

• Wang told her teacher Yang that she observed 9 emblems and 1 peony but did not say which one was peony. Teacher Yang concluded that, irrespective of the making of the coins, every coin on the table had an odd of 9 to 1 with emblem side up.

In this case, Zhang was caught in the fight between the "frequentist school" and the “Bayesian school". He did not know whether this was a result of an asymmetric making of the coin (the view held by the frequency school) or a result of merely bad luck, meaning various complicated factors contributed to this result in a completely random way (the view held by the Bayesian school). If Zhang tossed the coins 10,000 times and still got 9,999 emblems, the frequency school would argue that an imbalanced coin with confidence, while the Bayesian school would argue that the trials might be affected by complex environmental condition such as wind.

Wang may possibly be a practitioner of applied mathematics. As a believer of Kolmogorov's theory, Wang understands that all the probabilities are gone after the experiment. On the other side, Yang was likely a statistical physicist facing missing information. He believed that symmetry and identical coins are the key to the prediction of coins on the table.

Probability and randomness in physics, philosophy, and economics

With progress of knowledge, people in the 21st Century now have many new reflections on the understanding of Newtonian mechanics and related probability. For instance, mechanics is divided into kinematics and dynamics. The former focuses on describing movements and does not explain where movement comes from. This is similar to applied mathematics, which focuses on providing mathematical interpretation of movements. Dynamics, on the other hand, explains the relation between movement and force and focuses on causality. It is similar to theoretical physics and philosophy in this regard.

Take accelerated speed in the traditional system of Newtonian mechanics as an example: a=F/m, where F is the force, an external stimulus, which causes a body to accelerate; m is the mass of the body, the internal cause of movement. Here, accelerated speed is the "result" of the combined action of external and internal cause. But is this really true? In his speech, Professor Qian quoted Scottish philosopher David Hume. Many people hold that there is causality between two things that always happen in succession and tend to explain every phenomenon with causality. This is only a partial observation. Just because A is always seen to follow B doesn't mean there is causality between them. Later, the Einstein’s research has proven that the division of force and mass is unreliable when the moving speed approaches the speed of light. The classical and simple causality has been found to have limitations by modern physicists. Thermodynamics also raised new questions for Newtonian mechanics: "Entropy production" indicates the passage of time and the direction of time, that is, the derivation direction of causality.

Besides these physicists, philosophers such as Descartes, Popper and Kuhn have made outstanding contributions to our understanding of randomness and causal determination in science. Furthermore, economists such as Keynes, also distinguished between probability risk and uncertainty. The former is a measure of possible events, while the latter is our utter ignorance of possible future events. A rational person may exhibit completely different behaviors when facing probability risk and uncertainty.

Given these new understandings, we may see that what really matters is not whether a thing is possible, but how likely it is to happen. A lot of things may happen. But only what really happens becomes a fact. We should not take these facts for granted; instead, we should understand that there were many "possibilities" and "randomness". Such randomness still exists at present and may continue to impact our future. Can a person turn into a butterfly? Does the sun always rise in the east? We have no definite answer to these questions. But we can reach a level of certainty based on probability.

Qian further pointed out that probability is not a property of a body. Rather, it is a property of the dynamics of a system (dynamical system). Through observing the properties of such a recurrent system, we can draw a certain conclusion (a set of numbers) using the statistical method, so as to predict various complicated future situations. But Mark Twain said that any set of such numbers (statistical probability) was deceptive because it reflected the hypothesis，often hidden， of the statistician.

It is incomplete and difficult to grasp. We will still be able to find the "truth" to a certain extent by making the hypotheses as clear as possible, however, and use it to improve our understanding of the world. For example, drawing on the idea of "dynamical system", physicists hypothesized a " recurrent world", in which each and every event will repeat indefinitely thus the limit of frequency becomes the probability.

Conclusions

In the last part of his talk, Qian suggested a scenario in which an old wise man and a child are having a conversation and the child is supposed to keep asking, mechanically, “Why?” until the old man is rendered speechless. Undoubtedly, we should always seek the ultimate truth. But should we do this "infinitely"? Or should we ask "Why?" with moderation, make bold assumptions, verify them carefully, remain humble to methodology, respect randomness, and be cautious about the pursuit of truth? This might be worth considering.

In the question and answer session, Qian and Bai had a discussion about the relationship between randomness, applied mathematics, and theoretical physics, and gave insightful answers to questions raised by the audience. There was an interesting argument that asserted if we hold that all scientific theories have hypotheses, then is science really different from other activities to understand the world? How should we respond to scientism and its claim to be the gold standard that is closest to the "truth"?

Qian and Bai mentioned that Popper regarded "falsifiability" as a critical aspect of discerning science. Science is neither mysterious nor superior, though it enjoys advantages in dealing with many problems. In an era where ancestors, religions, and gods are all losing ground, science has become something we invest our hope in; it is a set of consistent explanations that allow us to live in peace. We need science to provide a "certainty" for our lives that can reassure us. But we should always keep in mind the "uncertainty" and "randomness" throughout life’s long history. In other words, the pursuit of "certainty" is understandable, whereas science provides somewhat satisfying explanations of things in the present. When it comes to questions like what is "truth” and does it even really exist independent of belief, we should keep an open and inclusive mind, and respect science as well as other important forms of knowledge.

Original article in English by Zhilin Li